Wprowadzenie do budowy heterogenicznego komputera kwantowo - klasycznego

dr inż. Łukasz Herok, lukasz@lukaszherok.com

Artykuł ten dostarcza podstawowych informacji o komputerach kwantowych. Omawiane są podstawy fizyczne na który komputer kwantowy działa. Wskazywane są potencjalne pola zastosowań. Przedstawiono również wybrane cztery układy na bazie których budowane są kubity oraz pokrótce omówiono zasady ich działania.

Wiele wskazuje na to, że komputery przyszłości będą komputerami mieszanymi. Po części komputerami klasycznymi, działającymi na dobrze znanych nam bitach, a po części komputerami kwantowymi, działającymi na kubitach [1]. Część klasyczna będzie odpowiadała za kontrolę nad całością prowadzonych obliczeń i wykonywania dobrze nam znanych już algorytmów. Jej bardzo ważnym zadaniem będzie również dokonywanie korekcji błędów układu kwantowego. Natomiast podzespół kwantowy (Rys. 1), będzie przeznaczony do wykonywania dedykowanych algorytmów tak zwanych algorytmów kwantowych, które nie mogą być w realnym czasie przetworzone przez procesory bitowe. Sformułowanie komputer kwantowy sprowadza się w takim razie nie urządzenia jako całości ale do podzespołu odpowiedzialnego za obliczenia kwantowe, analogicznie jak ma to już dziś miejsce z innymi układami zoptymalizowanymi dla danej klasy obliczeń, na przykład kart graficznych.

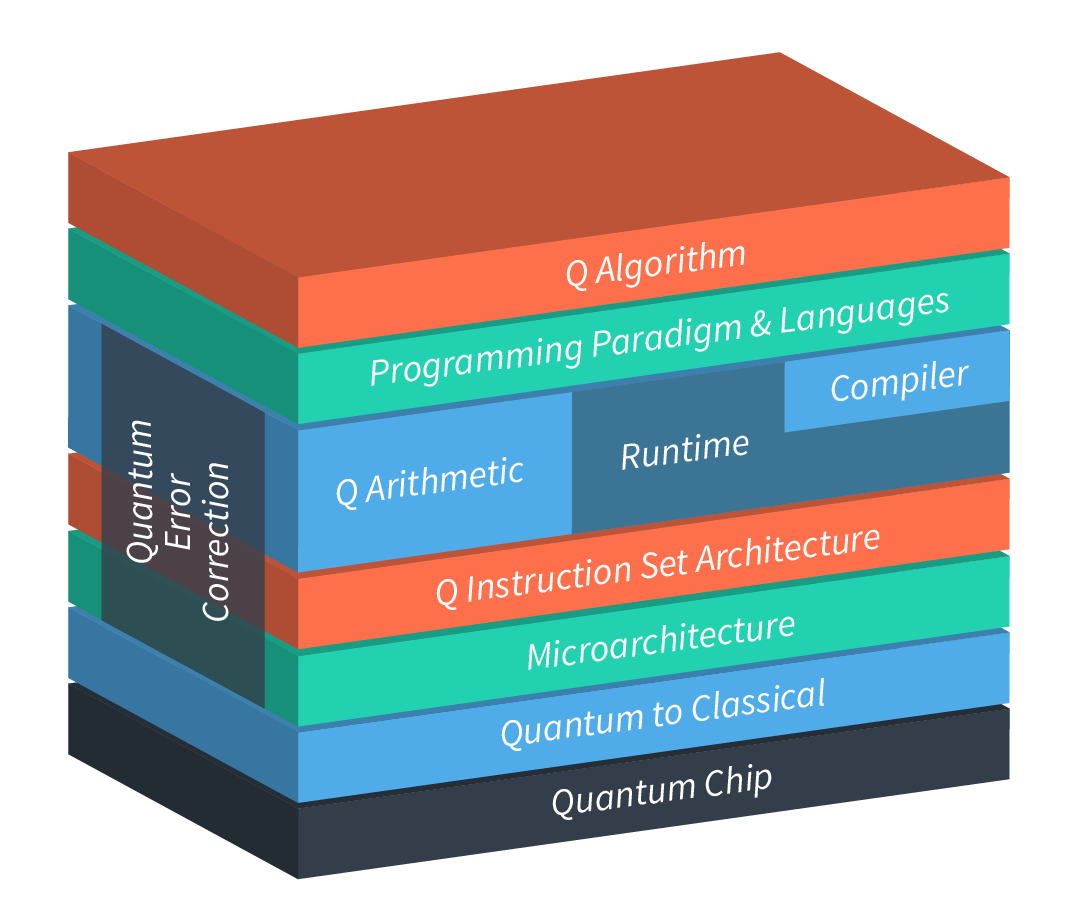
A generic square placeholder image with rounded corners in a figure.
(Rys. 1) Proponowana architektura układu kwantowego [1]

Zastosowanie akceleratorów kwantowych

Chipy kwantowe, mogą przetwarzać specjalnie dla nich przygotowane algorytmy. Pierwszym z nich była Kwantowa Maszyn Turinga [2]. Na dzień dzisiejszy opracowanych jest kilkadziesiąt algorytmów kwantowych [3]. Najbardziej znanym algorytmem jest algorytm Shora za pomocą którego można dokonać faktoryzacji bardzo dużej liczby. Pole jego zastosowań to przede wszystkim kryptografia. Sam algorytm Shora jest algorytmem który do działania wymaga współpracy komputera klasycznego i kwantowego. Potwierdza to hipotezę przedstawioną we wstępie.

W teorii każdy algorytm kwantowy może być zaimplementowany i uruchomiony na komputerze klasycznym. W tej chwili do programowania algorytmów kwantowych można używać symulatorów zaimplementowanych na komputerach klasycznych. Niestety wykonanie takiego algorytmu jest wysoce nieefektywne i może trwać dziesiątki lat, gdzie w przypadku chipu kwantowego wynik możemy otrzymać w zasadzie od ręki. Wzrost prędkości obliczeń można sprawdzić w [3].

Podstawy fizyczne

Zasada działania jednostki kwantowej opiera się na dwóch zjawiskach fizycznych: superpozycji stanów i splątania kwantowego. Klasyczne komputery operują na bitach, które mają dwa jednoznacznie określone stany: 0 lub 1. Natomiast w komputerze kwantowym wykorzystywane są kubity. Potrafią one przyjmować nie tylko dwa z góry zdefiniowane stany. Działają one w przestrzeni stanów, gdzie bazowe stany opisujemy jako: \(|0>\) i \(|1>\), jednak w odróżnieniu od bitu, kubit może znajdować się w superpozycji tych dwóch stanów \( |\psi> = \alpha|0> + \beta|1> \), gdzie \(\alpha, \beta\) to liczby zespolone, których kwadrat \(|\alpha|^2, |\beta|^2\) określają prawdopodobieństwo wykonania pomiaru o wyniku \(0\) albo \(1\) odpowiadających stanom \(|0>\) i \(|1>\). Należy pamiętać, że muszą one spełniać warunek normalizacji, tzn. \(|\alpha|^2 + |\beta|^2 = 1\). Geometrycznie stan kubitu można zaprezentować za pomoc sfery Blocha (Rys. 2).

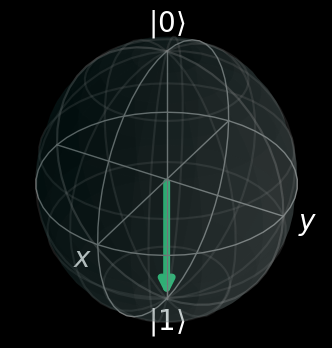
A generic square placeholder image with rounded corners in a figure.
(Rys. 2) Sfera Blocha. Na biegunach znajdują się stany bazowe, a na powierzchni kuli znajdują się pozostałe, czyste stany kwantowe.

W komputerach klasycznych bity łączymy w bajty. Taki zestaw połączonych bitów potrafi w danej chwili przechowywać tylko jedną informację - jeden stan układ. Sprawa ma się inaczej gdy użyjemy kubitów. Wykorzystując zjawisko splątania kwantowego, łączymy je w większe układy. W przypadku takiego splątanego układu kubitowego dysponujemy stanem który jest faktycznie superpozycją wszystkich możliwych stanów tego układu. Na przykład \(|\psi> = \alpha_0|0...00> + \alpha_1|0...01> + ... + \alpha_{{2^n}-1}|1...11>\). mieści w sobie informację nie o jednym stanie, ale \(2^n - 1\). Czyli na przykład układ dwukubitowy może znajdować się w superpozycji 4 stanów bazowych: \(00, 01, 10 i 11\). Należy pamiętać, że stan splątany nie może być zdekomponowany w oddzielne, pojedyncze stany kubitowe i zapisany jako iloczyn tensorowy stanów jedno-kubitowych.

Przykładowo stan \(\begin{bmatrix} \alpha\gamma \ \alpha\delta \ \beta\gamma \ \beta\delta \end{bmatrix}\) nie jest stanem splątanym, ponieważ można go zapisać jak iloczyn tensorowy \(|\psi> \otimes |\phi>\) dwóch wektorów: \(|\psi>= \begin{bmatrix} \alpha \ \beta \end{bmatrix}\) i \(|\phi>= \begin{bmatrix} \gamma \ \delta \end{bmatrix}\) Natomiast stany: $$|\phi^+> = \frac{|11> + |00>}{\sqrt{2}}$$ $$|\phi^-> = \frac{|11> - |00>}{\sqrt{2}}$$ $$|\psi^+> = \frac{|01> + |10>}{\sqrt{2}}$$ $$|\psi^-> = \frac{|01> - |10>}{\sqrt{2}}$$

Są stanami splątanymi ponieważ nie można ich zapisać jako iloczyn tensorowy dwóch wektorów. Zaprezentowane wyżej stany są to stany Bella. W podanym zapisie w każdym ket na pierwszej pozycji występuję stan pierwszego kubitu, na drugim miejscu kubitu drugiego. Wszystkie z wyżej wymienionych par Bella wykorzystywane są w informatyce kwantowej, jednak najczęściej używany jest \(|\Phi^+>\) , który można zapisać równoważnie, do podanej wcześniej notacji \(\begin{bmatrix} 1 \ 0 \ 0 \ 1 \end{bmatrix}\) .

Dzięki wykorzystaniu superpozycji stanów oraz splątania kwantowego możemy budować układy kubitowe w których przestrzeń stanów, szybko rośnie wraz z ilością dostępnych kubitów. Daje to możliwość wykonywania obliczeń o złożonościach niedostępnych dla komputerów klasycznych.

Wymagania techniczne

Na dzień dzisiejszy wyzwaniem jest zbudowanie jednostek z coraz większej ilości splątanych ze sobą kubitów. Układ taki musi dawać możliwość ustawiania wartości i odczytu stanu pojedynczego kubitu z wykorzystaniem zestawu uniwersalnych bramek. Oczywiście musimy pamiętać o tym, że zgodnie z zasadami mechaniki kwantowej pomiar stanu powoduje złamanie funkcji falowej i zniszczenie superpozycji stanów, dlatego pomiarów nie można dokonywać w sposób bezpośredni, bo spowoduje to utratę informacji. Wpływ czynników zewnętrznych oraz oddziaływanie kubitów między sobą również jest powodem zniszczenia stanu kwantowego w układzie, czyli do dekoherencji kwantowej. Im dłuższy czas dekoherenecji układu tym lepiej, ponieważ jest to okno czasowe w ramach którego algorytm kwantowy musi zakończyć swoje działanie. Opisane powyżej kryteria, jakie powinien spełniać komputer kwantowy, zostały nakreślone przez DiVincezo w roku 2000 [4].

Rodzaje kubitów

Akcelerator kwantowy, który faktycznie będzie potrafił potrafił wykonywać złożone operacje będzie musiał składać się z milionów kubitów. Dlatego z punktu widzenia skalowalności konieczne jest wybranie właściwego materiału czy też układu fizycznego oraz opanowanie technologii jego powtarzalnego wytwarzania.

Chip kwantowy może być zbudowany z różnych materiałów. Najbardziej znanymi na dzień dzisiejszy implementacjami są kubity:

Właściwościami termodynamicznymi, za pomocą których możemy badać przydatność materiałów pod kątem zastosowania jako kubity są: temperatura, pole elektryczne, pole magnetyczne.

Kubity spinowe Ich działanie opiera się na możliwości kontroli i odczytu spinu wyizolowanego elektronu. Elektrony te są uwięzione w tak zwanych kropkach kwantowych. Taka pojedyncza kropka kwantowa tworzy pojedynczy kubit. Wyizolowanie elektronu polega na tym, że tworzymy studnię potencjału i na jej wejściu obniżamy poziom energii tak, aby możliwe było wskoczenie do niej tylko elektronu o spinie skierowanym w dół (ma niższą energię). Zasada Pauliego zapewnia, że w kropce kwantowej znajdzie się tylko jeden elektron. Odczyt końcowy działa na podobnej zasadzie. Odpowiednio sterujemy potencjałem na wyjściu, tak aby kropkę kwantową mógł opuścić tylko elektron o spinie skierowanym w górę. Tą metodę odczytu nosi nazwę Elzerman readout. Kubity spinowe muszą działać w niskich temperaturach, tak aby energia termiczna nie przewyższała energii elektrycznej, którą sterujemy kubitem. Sąsiadujące kropki czują swoją obecność przy zmianie ładunku. Z tego powodu aby móc je lepiej izolować konieczne są dodatkowe bramki wyrównujące potencjały pomiędzy nimi. Sterowanie kubitem realizowane jest poprzez wykorzystanie pól magnetycznych. Poddając kropkę kwantową zewnętrznemu, statycznemu polu magnetycznemu dochodzi do wydzielania się poziomów energetycznych (Zeeman splitting). Następnie do kontroli stanu kubitu wykorzystuje się zmienne pole magnetyczne o kierunku prostopadłym do zadanego wcześniej zewnętrznego pola magnetycznego (oscylacje Rabi’ego). W ten sposób implementowane są bramki jednokubtiowe. Zaletą kubitów spinowych jest ich długi czas konherencji oraz wysoka gęstość upakowania.

Kubity Nitrogen-vacancy centers Materiałem wykorzystanym do budowy tych kubitów jest diament i występujący w nim defekt punktowy. Bazują one na spinie jądra, a stowarzyszony z nim elektron daje dodatkowe możliwości przechowywania danych. Stan kubitu odczytywany jest za pomocą pomiaru emitowanej fali elektromagnetycznej. Różna długość fali związana jest ze spinem w dół i w górę. Splątanie dwóch kubitów odbywa się poprzez naświetlenie laserem pierszego i drugie centrum NV. Następuje emisja fotonu poprzez elektron w centrum NV. Pozwalamy emitowanym z nich fotonom interferować. Poprzez ich pomiar powodujemy splątanie dwóch centrów NV. Zaletami tego rodzaju kubitów jest to, że posiadają one długie czasy koherencji i mogą pracować w dużym zakresie temperatur, nawet w temperaturze 250 K. Są one obiecującymi kandydatami do zastosowań w internecie kwantowym.

Kubity nadprzewodzące Nadprzewodnictwo jest to efekt kwantowy, który jest obserwowalny makroskopowo. Wydaje się więc ono naturalnym kierunkiem przy budowie komputerów kwantowych. Kubity nadprzewodzące są budowane jako elektrodynamiczne obwody nadprzewodzące, do opisu których nie używa się klasycznych pojęć prądu i napięcia, ale funkcji falowej jej amplitudy i fazy. Przykładem kubitu nadprzewodzącego jest transmon (Rys. 3.). Zalicza się on do nadprzewodzących kubitów ładunkowych. Wykorzystane w nim złącza Josephsona pozwalają rozwarstwić harmoniczne spektrum energii, tak aby można było łatwo wyróżnić dwa stany: podstawowy i pierwszy wzbudzony. W transmonie odczytów dokonujemy poprzez złącza readout resonators. W zależności od stanu kubitu na wyjściach obserwujemy przesunięcie w częstotliwości rezonatora. Aby wyeliminować szum przy odczytach dokonuje się wielu odczytów i z histogramu odczytywana jako wartość wynikową ta która miała zarejestrowanych najwięcej zliczeń. Operacje kubitowe realizowane są z wykorzystaniem oscylacji Rabi’ego poprzez użycie zewnętrznego oscylujące pola elektrycznego. Rotacji w płaszczyźnie X-Y dokonujemy poprzez krótkie impulsy o poprawnej fazie, amplitudzie i długości. Parowanie qubit-qubit realizowane jest poprzez specjalną szynę rezonująca łączącą kubity. Aby utworzyć stan splątany konieczne jest użycie bramek dwukubitowych np. CNOT.

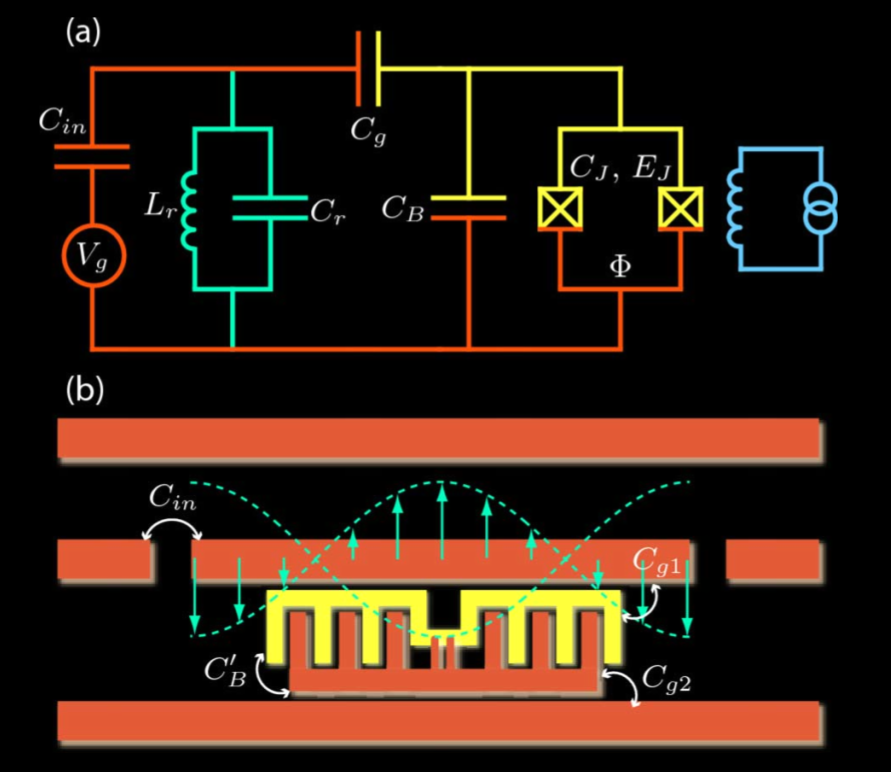
A generic square placeholder image with rounded corners in a figure.
(Rys 3.) a). Diagram obwodu tworzącego transmon b) Uproszczony schemat prezentujący budowę transmonu [5].

Kubity topologiczne Bazują one na kwazicząsteczce nazywanej fermionem Majorany, która jest jednocześnie swoją antycząsteczką \(\gamma = \gamma^\dagger\) . W wyniku połączenia się dwóch Majoranów możemy otrzymać elektron lub nie otrzymać elektronu. Nadprzewodniki są dobrym środowiskiem do wytwarzania cząstek Majorany, gdzie formowane są one poprzez dziurę i elektron. Operacje kwantowe na kubitach topologicznych wykonywane są poprzez przeplatanie. Kubity topologiczne są obiecującym kierunkiem badań, ponieważ są one mniej czułe na zaburzenia pochodzące z zewnątrz w porównaniu do innych rodzajów kubitów.

Podsumowanie

Zbudowanie komputera, który będzie potrafił przetwarzać algorytmy kwantowe jest jednym z największych i najciekawszych wyzwań naukowo inżynieryjnych dzisiejszych czasów. W artykule przedstawiono fizyczne podstawy działania akceleratora kwantowego oraz wymieniono jego przykładowe implementacje.

Bibliografia